Physics 214 - Prelab 1¶
Interference and Diffraction¶
Name:
Section:
Date:
Your TA will collect this paper at the beginning of your lab section.
The basic problem is shown in the following figure, which represents light of a given wavelength \(\lambda\) passing through two slits separated by a distance \(d\). The distance to the screen is \(L\). In this lab experiment you will measure the intensity at a position \(y\) along the screen, which corresponds to a scattering angle \(\theta\).
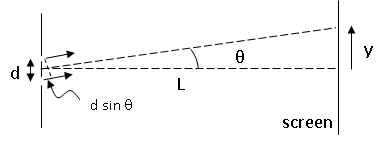
Fig. 1 Fig. 1¶
As shown in class, the phase difference between the two light beams at position \(y\) is:
is the path difference between the two beams. From phasor analysis, if the intensity arriving at the screen from each slit is \(I_1\), the total intensity at \(y\) from both slits is:
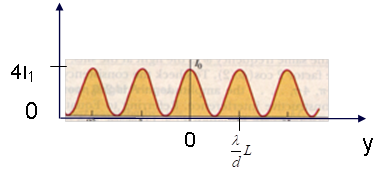
Fig. 2 Fig. 2¶
The more general form for the interference pattern from \(N\) slits is: \(I = I_1\left(\frac{\sin(N\phi/2)}{\sin(\phi/2)}\right)^2\).
1.¶
Show that this reduces to the 2-slit case when \(N = 2\).
When we consider the diffraction of light through a single slit of width a, we find that the single-slit intensity, \(I_1\), in the above equation is not simply a constant but also depends on angle. The single-slit pattern looks like the following plot:
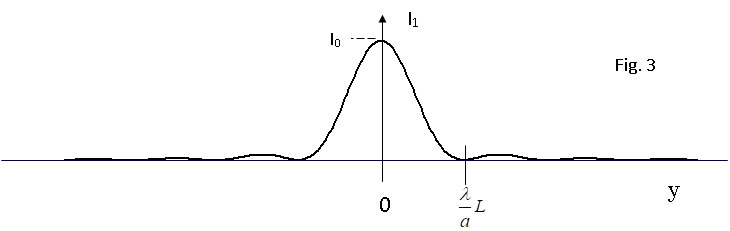
Fig. 3 Fig. 3¶
Answer:
2.¶
Calculate the position of the first diffraction minimum assuming a laser wavelength of 633 nm, a slit width of 20 \(\mu\)m, and a screen distance of 1 m.
Answer:
!!DO NOT FORGET TO INDICATE UNITS FOR ALL NUMERICAL ANSWER YOU PROVIDE!!
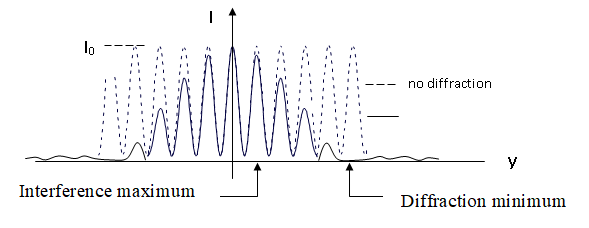
So the net result due to both interference and diffraction is the product of the curves in Figs. 2 and 3 (see also 214 Lecture 3):